
Relativity Myths & Ideas
Spacetime 101 - A Relativity Primer
Relativity involves a number of ideas that are not intuitive. It is important therefore to ensure that the basic concepts and terminology are clearly understood...
Coordinates and Reference Frames
Reference frames are a form of coordinate system. Two objects that are stationary with respect to each other are said to occupy the same "rest frame". Objects which are moving with respect to each other are in different rest frames. Special relativity only deals with inertial frames, i.e. ones that are in uniform linear motion with respect to each other.
Coordinate Time and Distances
Coordinate time and distances are the time intervals and spatial distances that would be measured in a given reference frame between any two events. They are called "coordinate" time and distance to indicate that they depend on the coordinate system in which they are measured, i.e. they can be different when measured in different reference frames. Such differences in elapsed time have been shown to exist empirically, which supports Einstein's theory that there is no absolute passage of time nor absolute space.
This effect is described in the Twin Paradox scenario, where one twin (who travels at near-light velocity away from and then back to the Earth) ages slower than his twin (who remains on the Earth).
Differences in Simultaneity
Einstein's Special Theory suggests that events that are simultaneous when viewed from one frame of reference may not be simultaneous when viewed from a different reference frame. However, such differences can not arise between events that are co-located, nor if they are causally related. Furthermore they have not been shown to exist empirically. Hence, they should not be confused with the differences in coordinate time intervals mentioned above.
Differences in simultaneity are described in the Einstein's Train scenario.
The Lorentz Transformation
The Lorentz transformation is used to translate coordinate time intervals and spatial distances between frames of reference. It is generally expressed in two formats; one describing time dilation and the other distance contraction. The two equations are mathematically interchangeable, and are commonly used together. The mathematics of the transformation is explained in more detail in Appendix A.
Spacetime
Spacetime is conceptually based on intervals, which may be loosely described as the "distance" in four dimensional spacetime between one event and another. Spacetime intervals are the combination of the coordinate time interval and spatial distance betwen two events. To combine time intervals and spatial distances, the units need to be compatible. E.g. Measuring the time in seconds, and the distance in light-seconds is compatible. Note: A light-second is nearly 300,000 Km - the distance that light travels in a second.
Spacetime intervals may be:
- Timelike - If the coordinate time interval between two events is larger than the spatial distance.
- Spacelike - If the coordinate spatial distance between the events is larger than the time interval.
- Zero - If the coordinate time interval and spatial distance are the same magnitude. Or...
- Lightlike - Only light and other electromagnetic phenomena can have lightlike intervals. Lightlike intervals are always zero, but not all zero intervals are lightlike.
Which is logical enough, however, in a given reference frame:
- Events that are simultaneous will have a spacelike spacetime interval.
- Events that are spatially co-located will have a timelike spacetime interval.
- Events that are simultaneous and spatially co-located will have a zero spacetime interval. But...
- Events that are neither simultaneous nor spatially co-located can have a spacelike, timelike or zero spacetime interval.
And therein lies the problem in understanding spacetime: The way that coordinate spatial distances and time intervals combine for events that are neither simultaneous nor co-located does not correspond to our everyday experience of space and time. The mathematical equation which describes this is explained in Appendix B.
A more technical introduction to spacetime may be found here.
Spacetime Diagrams
Spacetime diagrams are used to express spacetime relationships. The simplest way of doing this is with time shown as the vetical axis and spatial distances horizontally. The time interval and spatial distance can then be combined to derive the corresponding spactime interval. However, when time intervals are being mapped against spatial distances what are often being displayed are coordinate values, rather than spacetime ones.
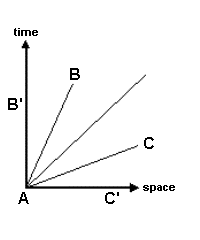
For example, an event such as person A clapping may be separated in space and time from persons B and C clapping, In the case of B, the coordinate time lapse is larger than the spatial distance. The resultant spacetime interval (B') lies along the time axis, and is timelike. Whereas for C the coordinate spatial distance is larger than the time lapse, So the spactime interval (C') lies along the space axis, and is spacelike.
Note: The line on the graph at 45 degrees represents relationships for which the coordinate time lapse and spatial distance are the same magnitude.
3D Diagrams
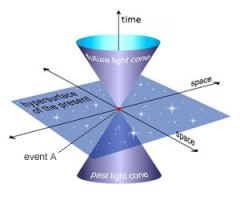
Spacetime diagrams are often represented three dimensionally, with time shown as the vertical (z) axis and space represented by the horizontal (x and y) axes. I.e. One of the spatial dimensions is suppressed to allow time to be included in the 3D representation.
In this 3D diagram, the line at 45 degrees becomes two cones which are referred to as "light cones". The front cone stands point downwards. The back cone stands with its point upwards. Event A is at the point where the two cones meet.
Events within the front cone are timelike (with respect to A) and could be caused by event A. Events in the back cone are also timelike (with respect to A) and are past events that could have caused event A.
Events outside the cones are spacelike (with respect to A) and can neither cause, nor be caused by, event A. The surface of the two cones represent the spacetime points where the spatial and time intervals are exactly the same (with respect to event A).
Proper Time
Proper time is a name given to a "timelike" spacetime interval between two events that would be recorded by a clock that is co-located with the events. Under special relativity, there is only one frame of reference in which the events are co-located. So the proper time interval between them is unique, and because the events are co-located, it is frame invariant. Under general relativity the proper time depends upon the path taken by the clock between the two events. There are many paths that can be taken, therefore the proper time interval is not unique. So is proper time a complete and absolute measure of time?
Well, we noted under coordinate time that, according to Einstein's theory, there is no absolute passage of time. So proper time is a consistent measure of time. However, the proper time interval between two events equates to myriad different coordinate time intervals as measured in different rest frames.
E.g. The proper time interval of 4 seconds measured by a clock at rest in the frame of reference in which two events are co-located equates to:
- A coordinate time interval between the events of 5 seconds in a frame of reference in which there is a spatial distance between them of 3 light seconds, and...
- A coordinate time interval between the events of 10 seconds in a frame of reference in which there is a spatial distance between them of 9.17 light seconds, and...
- A coordinate time interval between the events of 20 seconds in the rest frame where there is a spatial distance between them of 19.60 light seconds, and so on...
Hence, rather than being a complete and absolute measure of time, proper time is a consistent sub-set of coordinate time.
A more technical introduction to Proper Time may be found here.
Zero Spacetime Intervals
It is very easy to misinterpret the meaning of a zero spacetime interval. What it signifies is that light travelling towards A would move radially along the surface of the back cone, until it reached A. Similarly, light travelling away from A would move radially along the surface of the front cone until it reached event B. In both cases, the resulting spacetime interval is zero.
We might assume that that a zero spacetime interval means that there is no time passage, nor spatial distance, between the emission and absorption of the light. However, we can illustrate with a thought experiment that this is not necessarily the case...
A Flashlight Example
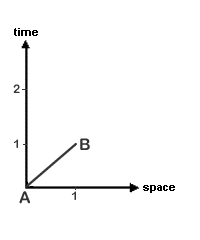
Two observers, Alfie and Betty, have a flashlight each and are mutually at rest one light-second apart. Alfie flashes his torch, and this is event A. Betty flashes her torch a second later, and this is event B. To light passing from event A to event B, these events may be regarded as being simultaneous and co-located. But Alfie and Betty do not experience them in that manner. A second after Betty flashes her torch Alfie will see the flash. As Betty is a light-second distant from him, Alfie knows that the light took a second to reach him. Hence Alfie concludes that event B happened a second after event A. So Alfie experiences the flashes of light as happening a second apart in time, and a light-second apart in distance.
This means that zero spacetime intervals do not necessarily mean that the events are simultaneous and co-located. To macro objects, a zero spacetime interval just means that the spatial and temporal "distances" beween two events are the same magnitude. So two events could be co-located and simultaneous, or be a thousand light-years distant and separated by a thousand years.
Furthermore, if this is true for zero intervals, it is also true for non-zero intervals. E.g. If a second after Betty flashes her torch, she flashes it again (event C):
- To the light passing from event A to event B, event A and event C are separated by a timelike spacetime interval of 1 second (the world line B to C).
- To Alfie, events A and C are separated by a distance of 1 light second, and a time interval of 2 seconds. I.e. They are neither simultanous nor co-located spatially.
So it would appear that spacetime only describes what takes place as viewed from frames of reference in which the events are simultanous or spatially co-located, (or both).
Limitations of the Concept of Spacetime
It follows from the flashlight example that spacetime neither describes nor conceptually encompasses what takes place as viewed from a frame of reference in which two events are neither simultaneous nor spatially co-located. If so, it would seem that the concept of spacetime, and hence general relativity, does not necessarily describe how macro objects experience space and time. Similarly, this suggests that spacetime, and general relativity, neither support nor deny the concept of differences in simultaneity (as suggested by the special theory).
Furthermore, as was noted under Proper Time, a spacetime interval between two given events is not only one of many possible spacetime intervals between those events, but is also just one of the myriad coordinate space and time relationships between the events.
Appendix A - The Lorentz Transformation
The Lorentz transformation can be expresed two ways:
The transformation for time intervals (t) is:
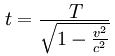
The transformation for spatial distances (x) is:
![]()
In these equations:
t is the coordinate time elapsed in the rest frame of the observer.
T is the coordinate time elapsed in the rest frame of the object.
x is the coordinate distance in the rest frame of the observer.
X is the coordinate distance in the rest frame of the object.
v is the relative velocity.
c is the speed of light.
Note: The two equations are mathematically interchangeable, and are commonly used together. However, it may be argued that they have distinctly different implications:
- If time dilates, less time passes in traversing a given distance, without distance contraction arising.
- If distances contract, less time is taken to traverse the shorter distance, without time dilation arising.
So in both cases less time passes, but for different reasons. Furthermore, in one case time dilates and in the other it does not. Hence the two descriptions may be regarded as alternative interpretations of the same mathematical relationship. We consider that possibility further under Time Dilation
Appendix B - Spacetime Intervals
Under special relativity, spatial distances combine according to the Pythagorean theorem. I.e.:
d2 = x2 + y2 + z2
where:
d is the coordinate spatial distance (in light-seconds).
x, y and z are the coordinate distances in the three spatial dimensions (in light-seconds).
Note: A light-second is nearly 300,000 Km - the distance that light travels in a second.
However, the square of the spacetime interval is the difference between the square of the coordinate time interval and the square of the coordinate spatial distance. I.e. For a timelike spacetime interval:
s2 = t2 - d2
where:
s is the spacetime interval (in seconds or light-seconds).
t is the coordinate time interval (in seconds).
d is the coordinate spatial distance (in light-seconds).
Under special relativity, the spacetime interval is unique, and correlates to the coordinate time interval measured in the frame of reference in which the events are co-located spatially, or the spatial distance in the frame of reference in which the events are simultaneous.
Under general relativity, the spacetime interval between events depends upon the path taken between them. Therefore it is not unique. However, the spacetime interval for any given path is frame invariant. It also equates to the coordinate time interval experienced by an observer who follows that path between the events.