Introduction
This site presents a non-mathematical overview of the re-working of Einstein's Special Theory of Relativity by John Field, who is a retired researcher at the University of Geneva, working at CERN. Starting from novel premises, and presented in an ongoing series of scientific papers, Field's analysis leads to the conclusion that time dilation arises without length contraction or differences in simultaneity. I.e. That special relativity is compatible with absolute simultaneity. However, and most controversially, this suggests that the Reciprocity Principle does not apply to special relativity.
This overview has been approved by John Field, who has kindly allowed his unpublished papers to be hosted on this site. These provide further insight into his ideas. Collectively, the published and unpublished papers represent a fundamental revision of the subject.
The Lorentz Transformation
John Field's paper "A New Kinematical Derivation of the Lorentz Transformation and the Particle Description of Light" distinguishes between the kinematic (i.e. space-time geometric) and the dynamic (i.e. concerning transformation laws of fields and forces) aspects of the transformation.
By this means he derives the Lorentz Transformation without assuming Einstein's second postulate (that the velocity of light is constant in all frames of reference). Instead, he uses three novel postulates to show that Einstein's second postulate is a necessary CONSEQUENCE of relativistic kinematics, if it is assumed that light consists of massless particles. The postulates are:
- A weak kinematical form of Einstein's first postulate (the Special Relativity Principle), that requires that space-time measurements in reciprocal experiments by two different inertial observers will be the same.
- Uniqueness. I.e. That the Lorentz Transformation should give a single solution for the description, in any frame, of a given space-time experiment.
- Spatial Isotropy. I.e. That space is uniform in all directions.
Particle/Wave Duality
Field also comments on the particle/wave duality of light. He deduces that, for consistency with Classical Electrodynamics, electromagnetic fields consist of large numbers of photons. The connection between wave-like behaviour in classical electrodynmics and quantum mechanics is explained in his paper "On the Relationship of Quantum Mechanics to Classical Electromagnetism and Classical Relativistic Mechanics".
John Field's paper "On the Relationship of Quantum Mechanics to Classical Electromagnetism and Classical Relativistic Mechanics" may be viewed or downloaded here.
Length Contraction and Relativity of Simultaneity
John Field discusses the presumed length contraction and relativity of simultaneity effects of Special Relativity in his paper "A sign error in the Minkowski space-time plot and its consequences". In it he describes how these ideas have become embedded in the literature.
Firstly, he explains how these effects were introduced into Einstein's original 1905 paper. This was simply a matter of important constants that were omitted from Einstein's equations. Einstein had pointed out the need for these constants, but he failed to include them in his own work. This resulted in the apparent length contraction and relative simultaneity effects. Adding the constants to Einstein's equations causes both to disappear.
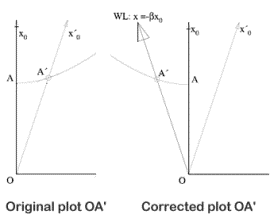
Field then shows how these same effects came to be included in graphical representations of the space-time relationships. This originated in a paper written by Minkowski in 1908. In a space-time diagram, derived by Minkowski, a world line OA' was rotated clockwise from OA, but should have been rotated anti-clockwise.
This had the effect of making it appear that the length of an object moving with respect to a given reference frame would contract when viewed at rest in that reference frame. Whereas, the corrected plot indicated that the length of the object remained the same.
Absolute Simultaneity & Invariant Lengths
As is noted under The Lorentz Transformation, John Field derived the Lorentz transformation by a novel method using postulates that differ from those used by Einstein. His derivation does not require, or suggest, that differences in simultaneity arise. Similarly, it does not invoke differences in physical dimensions or distances. In his words:
"It is demonstrated that the measured spatial separation of two objects, at rest in some inertial frame, is invariant under space-time transformations. This result holds in both Galilean and Special Relativity. A corollary is that there are no 'length contraction' or associated 'relativity of simultaneity' effects in the latter theory."
Instead he suggests that what is actually taking place is a difference in velocities. This suggests that the "Reciprocity Principle" does not apply to Special Relativity. Note: The Reciprocity Principle is the idea that if object A has a velocity of v with respect to the rest frame of object B, then object B has a velocity of -v in A's rest frame. This is true in Galilean Relativity, but it is not so in Field's interpretation of Special Relativity.
The velocity of the object B in A's rest frame is actually found to be -gamma v. In conventional special relativity time dilation is explained by length contraction (which implies relativity of simultaneity) and the Reciprocity Principle is respected. In Field's approach length intervals are invariant (which follows from translational invariance, independently of the form of the transformation equations) and there is no relativity of simultaneity. Time dilation is explained by the different relative velocities in the rest frames of A and B that do not respect the Reciprocity Principle.
John Field's paper "Absolute simultaneity and invariant lengths: Special Relativity without light signals or synchronised clocks" may be viewed or downloaded here.
The Reciprocity Principle
We noted under Absolute Simultaneity and Invariant Lengths that John Field came to the conclusion that the Reciprocity Principle did not apply to Special Relativity. Instead, he replaced the Reciprocity Principle:
"If the velocity of an inertial frame S' relative to another such frame S is v, then the velocity of S relative to S' is -v."
With a "Kinematical Reciprocity Principle":
The velocity of an inertial frame S' relative to an inertial frame S in primary space-time experiment is equal and opposite to the velocity of S relative to S' in the reciprocal experiment.
This uses the concept of primary and reciprocal scenarios, instead of reciprocal views of the same space-time experiment. Unlike the Reciprocity Principle, this Kinematic Reciprocity Principle is actually a definition of a pair of reciprocal experiments.
Having defined `reciprocal experiments' the "Measurement Reciprocity Principle" is postulated:
Reciprocal space-time measurements of similar rulers and clocks at rest in two different inertial frames S, S', by observers at rest in S', S respectively, yield identical results.
This is the first postulate Field uses to derive the Lorentz Transformation,, as noted under The Lorentz Transformation.
John Field's paper "Primary and reciprocal space-time experiments, relativistic reciprocity relations and Einstein's train-embankment thought experiment" may be viewed or downloaded here.